by

Logspace vs Polynomial time

One of the primary goals of complexity theory is separating complexity classes, a.k.a proving lower bounds. Embarrassingly we have only a handful of unconditional separation results. Separating P from NP is of course the mother of all such goals. Anybody who understands the philosophical underpinnings of the P vs NP problem would love to LIVE to see its resolution. Towards resolving this, we made some (“anti”)-progress (Eg : Relativization, Natural proofs, Algebrization) and have a new geometric complexity theory approach which relies on an Extended-Extended-Extended-Extended-Riemann-Hypothesis !! For more information about the history and status of P vs NP problem read Sipser’s paper [Sipser’92], Allender’s status report [Allender’09] or Fortnow’s article [Fortnow’09].

Today’s post is about the Logspace (L) vs Polynomial time (P) problem, which (in my opinion) is right next to the P vs NP problem in its theoretical importance. I guess many researchers believe that L \neq P. Did we make any progress/anti-progress towards resolving the L \neq P conjecture ?  Here are two attempts both based on branching programs and appeared in MFCS with a gap of 20 years !!

1) A conjecture by Barrington and McKenzie (BM’89): The problem GEN is defined as follows :

GEN : Given an n \times n table filled with entries from \{1,2,\dots,n\}, which we interpret as the multiplication table of an n-element groupoid, and a subset S of \{1,2,\dots,n\} which includes element 1, determine whether the subgroupoid <S>, defined as the closure of S under the groupoid product, includes element n.

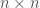
Barrington-McKenzie Conjecture : For each n > 1, a branching program in which each node can only evaluate a binary product within an n-element groupoid, branching n ways according to the n possible outcomes, must have at least 2^{n-2} nodes to solve all n \times n GEN instances with singleton starting set S.

The problem GEN is known to be P-complete [JL’76]. Barrington-McKenzie Conjecture would imply that GEN \notin DSPACE({{\log}^k}n) for any k. In particular, it would imply that L \neq P. I don’t know if there is any partial progress towards resolving this conjecture.

2) Thrifty Hypothesis : This is a recent approach by Braverman et. al [BCMSW’09] towards proving a stronger theorem L \neq LogDCFL. Stephen Cook presented this approach at Valiant’s 60th birthday celebration and Barriers Workshop. He also announced a $100 prize for solving an intermediate open problem mentioned in his slides.

Tree Evaluation Problem (TEP): The input to the problem is a rooted, balanced d-ary tree of height h, whose internal nodes are labeled with d-ary functions on [k] = \{1, . . . , k\}, and whose leaves are labeled with elements of [k]. Each node obtains a value in [k] equal to its d-ary function applied to the values of its d children. The output is the value of the root.

In their paper they show that TEP \in LogDCFL and conjecture that TEP \notin L. They introduce Thrifty Branching Programs and prove that TEP can be solved by a thrifty branching program. A proof of the following conjecture implies that L \neq LogDCFL. For more details, read this paper.
Thrifty Hypothesis : Thrifty Branching Programs are optimal among deterministic branching programs solving TEP.

Open Problems :

  • My knowledge about the history of L vs P problem is limited.  Are there other approaches/attempts in the last four decades to separate L from P ?
  • An intermediate open problem is mentioned in the last slide of these slides. The authors announced $100 prize for the first correct proof. Read their paper for more open problems.

References :

  • [BM’89] David A. Mix Barrington, Pierre McKenzie: Oracle Branching Programs and Logspace versus P. MFCS 1989: 370-379
  • [BCMSW’09] Mark Braverman, Stephen A. Cook, Pierre McKenzie, Rahul Santhanam, Dustin Wehr: Branching Programs for Tree Evaluation. MFCS 2009: 175-186
  • [Sipser’92] Michael Sipser: The History and Status of the P versus NP Question STOC 1992: 603-618
  • [Allender’09] Eric Allender: A Status Report on the P Versus NP Question. Advances in Computers 77: 117-147 (2009) [pdf]
  • [Fortnow’09] Lance Fortnow: The status of the P versus NP problem. Commun. ACM 52(9): 78-86 (2009) [pdf]
  • [JL’76] Neil D. Jones, William T. Laaser: Complete Problems for Deterministic Polynomial Time. Theor. Comput. Sci. 3(1): 105-117 (1976)

7 thoughts on “Logspace vs Polynomial time”

  1. Hello Kintali

    I haven’t solved that open problem despite many tries over the years. However a characterisation might interest you: L = NP iff read-only recursive programs are equivalent to read-only tail recursive programs, i.e., iff there is no need for the recursion stack in read-only computation.

    An earlier first-order version in TCS:

    http://portal.acm.org/citation.cfm?id=344414.319116

    A later higher-order version in JFP:

    http://portal.acm.org/citation.cfm?id=968494.968498

    Regards and good luck!

    Neil

    Reply

  2. Pingback: Separating Logspace from Polynomial time | Q&A System

  3. Im working on a variation of the P vs L problem & came up with the following formulation. I believe it has deep connections to the theory at best and at least is a nice general framework for studying time/space tradeoffs, complexity class separations, etc.; if anyone agrees its a valid open problem please upvote my question, Id appreciate it.

    http://cstheory.stackexchange.com/questions/9680/repetition-in-compressibility-of-tm-run-sequences

    my original idea that led to this was a proof sketch along the lines that if P==L then P!=NP. I am still debating whether to write up this proof sketch somewhere in cyberspace (cstheory moderators/audience didnt react favorably so far)

    Reply

  4. Pingback: Separating Logspace from Polynomial time | CL-UAT

  5. Pingback: Backurs, Indyk connect strong exponential time hypothesis to edit distance; other CS time/ space hiearchy/ continuum news | Turing Machine

Leave a comment