Today’s post is about TreeWidth. When I first came across treewidth, I became an instant fan.
Definition : A tree-decomposition of a graph
is a pair
where
is a family of subsets of
, one for each node of
, and
is a tree such that :
- The union of the sets
is equal to
.
- for all edges
, there exists an
with
and
.
- for all
: if
is on the path from
to
in
, then
.
The treewidth of a tree-decomposition is
. The treewidth of a graph
is the minimum treewidth over all possible tree-decompositions of
.
Following are some interesting facts :
- Exercise : TreeWidth of a tree is 1.
- Exercise : TreeWidth of a clique on
vertices in
.
- Determining whether treewidth of a given graph is at most
is NP-complete.
- See [BGHK’95] for interesting applications of treewidth Eg : Choleski factorization on sparse symmetric matrices.
- There is an analogous notion of pathwidth which is also NP-complete.
Approximating tree-width : Bodlaender et. al [BGHK’95] presented an factor approximation algorithm for treewidth. This also gives an
factor approximation algorithm for pathwidth. Their algorithm works by repeatedly finding vertex separators and uses Leighton-Rao’s algorithm at its heart. The main insights from their paper are as follows :
- If there is a factor
approximation algorithm for vertex separator then there is an
approximation algorithm for treewidth.
- if there is a factor
approximation algorithm for treewidth then there is an
approximation algorithm for pathwidth.
In 1995 the best known approximation factor for vertex separator was . Feige, Hajiaghayi and Lee [FHL’2008] improved this to
. Hence we have
and
factor approximation factors for treewidth and pathwidth respectively.
Special cases : What about computing treewidth of restricted classes of graphs ?
- When
is any fixed constant, the graphs with treewidth
can be recognized, and a width
tree decomposition can be constructed for them, in linear time [Bodlaender’96].
- Seymour and Thomas [ST’] showed that branchwidth of planar graphs can be computed in polynomial time. This implies a factor 3/2 approximation for treewdith of planar graphs.
Bounded TreeWidth : If the treewidth of a graph is bounded by some fixed constant
, then several problems (that are NP-hard (even PSPACE-hard) for general graphs) can be solved in polynomial-time and often linear time !! Some of them include Maximum Independent set (hence maximum Clique), Hamiltonian cycle, Graph Isomorphism. Instead of listing all these problems, lets look at the following awesome theorem.
Courcelle’s Theorem : Any property of graphs definable in monadic second-order logic (MSO2) can be decided in linear time on any class of graphs of bounded tree-width. In other words, MSO2 is fixed-parameter tractable on any such class of graphs.
Theorem [KT’2010] : If C is any class of graphs which is closed under taking sub-graphs and whose tree-width is not bounded by a poly-logarithmic function then MSO2-model checking is intractable on C (under suitable assumptions from complexity theory)
Open Problems :
- Perhaps the most interesting open question is to obtain a constant factor approximation for treewidth.
- Bodlaender et. al ruled out absolute approximation algorithm, (unless P = NP) for treewidth and pathwidth. This is the best known hardness. Can we even rule out PTAS for treewidth ? Note that the hardness of treewidth implies the hardness of vertex separator (with constant factor blow-up).
- How hard is computing treewidth of planar graphs ? NP-hardness is not known. Many researchers I talked to, believe that treewidth of planar graphs can be computed in polynomial-time.
- Can the lower bound from [KT’2010] be improved ? In this context, it is interesting to note that Maximum Independent Set can be solved in polynomial time even when the treewidth is bounded by
.
- Datta et. al [DLNTW’2009] showed that planar graph isomorphism is in logspace. Is isomorphism for graphs with bounded treewidth in logspace ? I asked this question to some researchers, and this seems to be an open problem.
References :
- [BGHK’95] Hans L. Bodlaender, John R. Gilbert, Hjálmtyr Hafsteinsson, Ton Kloks: Approximating Treewidth, Pathwidth, Frontsize, and Shortest Elimination Tree. J. Algorithms 18(2): 238-255 (1995)
- [Bodlaender’96] Bodlaender, Hans L. : A linear time algorithm for finding tree-decompositions of small treewidth. SIAM Journal on Computing 25 (6): 1305–1317 (1996)
- [KT’2010] Stephan Kreutzer, Siamak Tazari Lower Bounds for the Complexity of Monadic Second-Order Logic arXiv:1001.5019
- [FHL’2008] Uriel Feige, MohammadTaghi Hajiaghayi, James R. Lee: Improved Approximation Algorithms for Minimum Weight Vertex Separators. SIAM J. Comput. 38(2): 629-657 (2008)
- [ST’90] PaulD.Seymour and Robin Thomas : Call Routing and the Ratcacher. Combinatorica 14(2): 217-241 (1994)
- [DLNTW’2009] Samir Datta, Nutan Limaye, Prajakta Nimbhorkar, Thomas Thierauf, Fabian Wagner: Planar Graph Isomorphism is in Log-Space. IEEE Conference on Computational Complexity 2009: 203-214

Regarding your last question, see the STACS 2010 paper Restricted Space Algorithms for Isomorphism on Bounded Treewidth Graphs for a nice summary of the state of the art. In particular, answering your question, the authors show that the problem of deciding isomorphism of graphs with bounded treewidth is in LogCFL, which is in L (and therefore P). This improves the previous bound of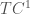 by Grohe and Verbitsky in 2006.
by Grohe and Verbitsky in 2006.
To correct my statement above: L NL
NL  LogCFL
LogCFL  P. So the problem remains open, with the gap slightly smaller than before.
P. So the problem remains open, with the gap slightly smaller than before.
Thanks for pointing out the STACS paper.
Can the 3/2-approximation for computing the treewidth of planar graphs be generalised for other minor-closed classes? In particular, for each t is there a constant c_t such that there is a c_t-approximation algorithm for computing the treewidth of graphs with no K_t-minor?
This question seems closely related to separators in graphs with no K_t-minor [Alon-Seymour-Thomas JAMS, Reed-Wood T.Alg, Kawarabayashi-Reed FOCS ’10].
Pingback: Graph Isomorphism and Bounded Tree Width « My Brain is Open
Pingback: Hardness of Graph Isomorphism of Bounded TreeWidth Graphs « My Brain is Open
Can you give some reference on “Many researchers I talked to, believe that treewidth of planar graphs can be computed in polynomial-time.”?
hi
i’m using treewidth to compute and edge coloring of graph of bounded arboricity. i’m looking for some classes of graphs with treewidth bounded from O(log n) or or more generally with sublinear bound…
do you know anything about that?
anyway tnx for your post, i think you’ve made a complete and smart presentation of the argument.
🙂
Pingback: Computing Bounded Path Decompositions in Logspace « My Brain is Open
Is the tree width of a graph on $n$ vertices upper bounded by the tree width of clique on $n$-vertices? Also how does tree width behave with respect to the disjunctive product?
— Yes.
— What is the disjunctive product of graphs ?
Pingback: Logspace algorithms on graphs with bounded tree width | CL-UAT